I’m not very good at math, I would like to be, but I’m really not. But I do enjoy playing with math on a pure amateur level.

One night my brain decided that it would get stuck thinking about primes that have a digit sum that is also prime. A simple example: 11 => 1+1 => 2 so 11 is in the sequence, while 13 => 1+3 => 4 is not. The first 20 primes whose digit sum are also prime are (with the digit sum below each prime):

2,3,5,7,11,23,29,41,43,47,61,67,83,89,101,113,131,137,139,151
2,3,5,7, 2, 5,11, 5, 7,11, 7,13,11,17,  2,  5,  5, 11, 13,  7

One interesting thing that jumped out at me when I did this was that there are prime digit sums that have prime digit sums that are prime. I.e we have chains of prime digit sums (for example 83 => 11 => 2). A natural question we have is “What is the longest prime digit sum chain?” We’ll come back to that later.

I wrote a little program and ordered myself the first 25 million primes to run the program on. The program simply eats a prime number and builds the chains of prime digit sums. Let’s take a look at the results!

In the 25 million primes, 9 350 225, around 37 percent, have digit sums that are primes! We could plot the distribution of how many times the digit sum is a certain number (not sure if this is remotely interesting but hey graphs!).

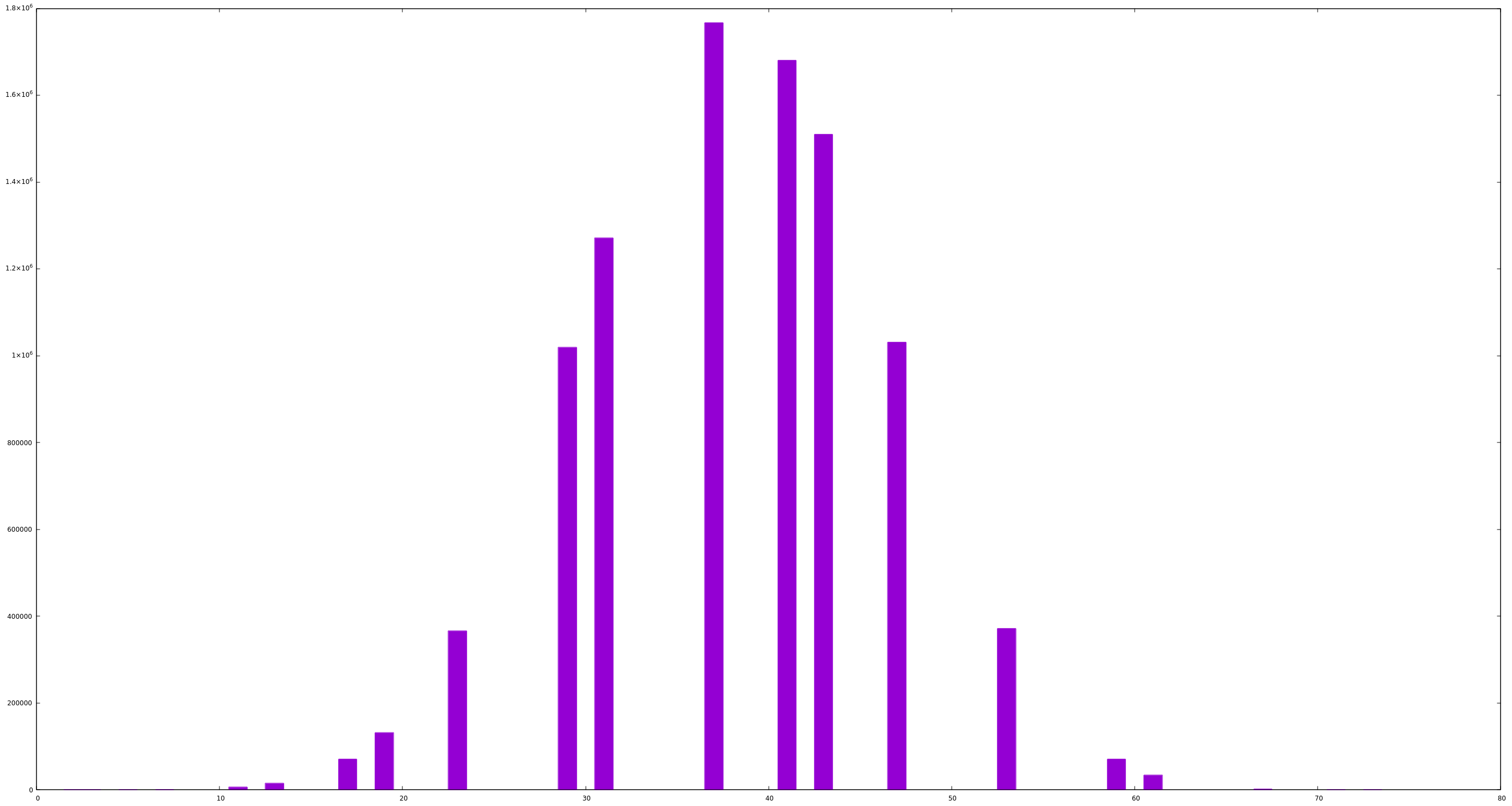
We see the expected result. There are more ways to make 37 than there are to make 2 (of which there are 3 of). Another thing we can see is that we are getting at least one of each of the primes up to 71.

Let’s get back to the question of prime digits sum chains. In the first 25 million primes the longest chains of length 3 ([29,11,2] and [47,11,2]). Of course the largest theoretical digit sum of a number of length n would be n*9 (i.e the largest 5 digit number is 99999 which has a digit sum of 45) and we haven’t looked at any particularly long primes here. To find longer prime chains we could for example look at some larger primes like the larger mersenne primes (I might do this if I get the time).

Some questions I’m left wondering (and probably will never know the answer to regardless of how “trivial” they seem I doubt I’ll ever have the mathematical knowledge to even attempt to prove them):

1. Are there infinitely many sum-primes? (This seems trivial but I don’t know how to prove it)
2. If you look at the list of primes that can be represented as the digit sum of other primes you seem to just simply get back the list of all prime numbers (in my experiment I got all primes from 2 to 71). Can all prime numbers be expressed as the digit sum of another prime?
3. What is the largest chain of prime sums that we can get? (seems obvious that we can just make longer primes and get longer chains but obvious does not equal true).

That’s enough mathematical numerology from me for a little while!